Introduction to Abstract Algebra

Lecture 1

Warm-up

Lecture 3

Warm-up

1. 
   False,
2. 
   False,
3. ?
   
4. Describeas a subset of.
   , the last digit isin base

Notation

iff

Z/nZ: Act II

Remark:consists of subsets of

Proposition

has exactly n elements

Proof

claim 1

if, then

Let, then


then,

claim 2

ifand, then[i] and [j] do not intersect

We prove by contradiction:
assume
then,

According to, we have
Since a and b are integers, we have
and since we have,


which caused a contradiction, and it should be. Proved.

claim 3

Everybelongs to one of the classes

Proof:
By,has at least n elements.
By,has at most n elements.

(Z/nZ,+)

Q: How to “add”and?
A:

Proposition 2

Addtion is correctly define on,the classis the same for diff. elements ofand.

Proof:

Lecture 4

Warm-up

For which a,b holds:

2.For which a,b holds:

Groups

(Z/nZ,+)

is a special element:
exists:

(generator|relations)

(Z/nZ,)

is a special element:
: not always multiplicative “inverse”
Warning:,, sometimes you do have inverse.

the same but only finite primes are used.finitely generated(just need finite generator to generate all of them)

Definition of Group

A groupis a set G and a binary operations.t.,

Associativity:
Identity:
Inverses:
PS: sometimes,is written as(more specific?)
Q: Why “groups”?
A1:
Symmetries of “objects”
it shouldn’t be only about groups!(CS: monoids:associativity+identity)
Q: What to do now?
A2:
to deduce something from associativity+ identity+ inverses
clarify something?

Homomorphism

Definition of Homomorphism

A homomorphism fromtois a map (of sets),s.t.

like

Lecture 5

Warm-up

1.
Ans:

2.Solve forin




3.What did we cover last time in class?

Groups:Basic Properties

Proposition

Identity element e is laways unique in any group G.

Proof. By contradiction


which caused a contradiction

Proposition 3.18

is a group. The inverseis unique

Proof: By contradiction


which caused a contradiction that

Proposition 3.19

For any

Proof:

Proposition 3.20

Proof:

Cor(Prop 3.21)

For any

Proof:

Proposition 3.22

Proof:

Subgroup

is subgroup of G generated by $$

Lecture 6

Warm-up

How many different ways to puton
Ans:

Symmetric Groups

Definition of Symmetric Groups

Letbe a set, we define(cardinality of X=number of elements in X) is a group of all bijective maps(bijections)

Operation on:


“compositionof functions” composition of maps

Proposition

Operation of composition (of maps) is associative
Identity:
Inverses:?

Examples:is a finite set.


has two elements.”transpositions”=maps which intercharges only tow elements.
has exactly 6 elements()
Q:How to think about elements of?
A_0: functions which are bijective.
A_1:“matrices”,

the first row: original set, the second row: image of

A_2: “strings”:
Example:,
Q: composition via strings?
“” first, second,

A_3: cycles presentation
Example:(1 goes to the 3, and 3 goes to the 1)
(1 goes to the 3, 3 goes to the 2, and 2 goes to the 1)

Inverses

just flip it

Lecture 7

Warm-up

1.Prove thatwithis a group.
Proof:
1.Associativity:

2.Identity:
0 serves as the identity, since
3.Inverses:
Every element have inverses. Inverse ofis, such that

2.How to find new examples of groups?
We can explore new groups by identifying subgroups of existing groups. Utilizing Existing Group Structures:
By adding constraints to existing groups, such as restricting certain properties (e.g., determinant = 1 for matrices), you can form new groups. The example ofandshows how restricting the determinant of matrices creates the special linear group.

Subgroups

Definition of Subgroups

is a group, Subgroupofis a groupwith the group operation restricted from.

About restrictions of functions:

Back to Subgroups:


Examples:
For every:
consists of, where,is “almost the same” ason.Andis not a subgroup od. Actually, operation is not the same(counterexamples:).

Definition

Subgroup diagram of a group,trival subgroup(),is contained as a set. They are all subgroups of

Definition of Proper Subgroups

Proper subgroup ofis subgroup which is not trivial oritself.

Proposition 3.30

is a subgroup ofiff:

1.(identity of subgroup)

2.(closure of the group operation)if, then,

3.(closure of inverses)if, then.

is Problem #2 on HW#3
is a subgroupthat all of three is true

Proposition 3.31

is a subgroup iff () and ()

Proof:(follows from 3.30):



is a subgroup in
:


Cancellation law on the right,

Lecture 8

Warm-up

Find all subgroups of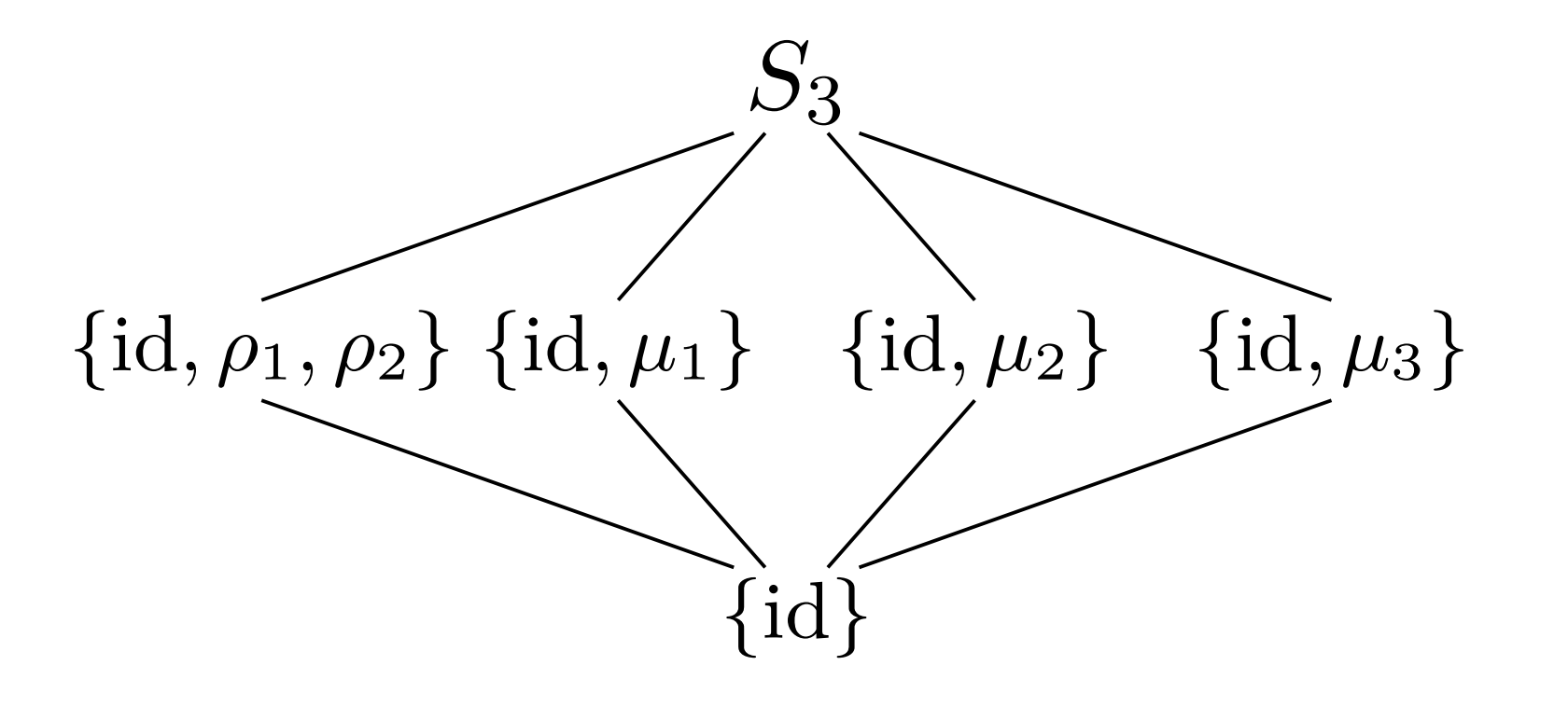

Notation

ifis a subgroup of, we write, and if

Cyclic Subgroups

if, we have

Definition

$Ga{a^k | k \in Z}\star = \star_G$

Lemma

$={a^k|Z}$ is a subgroup of G

Proof. By Prop3.31
if, then

Theorem 4.3

$H \leq G \quad s.t. \quad a \in H$

Proof:part is already proved.Let us prove the second part.Any subgroup, then
$$\forall k \in Z, a^k \in H, \text{then} \leq H$$
Therefore $HGa \in H$

Definition

,Order of $$ is minimal,s.t.

Notation:

Examples:

Definition

is cyclic iff $\exists g \in G, G=$

Example ?

Theorem 4.9

Every cyclic group is abelian,

Lecture 9

Warm-up

is defined by.Is it a homomorphism?(is all invertiblematrices with all entries from)
Maybe it’s not.

Ifis a homomorphism:



which is not true obviously.

Isomorphism

Definition

Isomorphism is bijective homomorphism.(which is bijective：injective,subjective)

Example:

Prop 11.4

are groups and they are homomorphism, then:
1.
2.
3.if, then(image ofunder)
3’. as, then(image of:)
4. if, thenis a subgroup of G (we callis called pre-image of)

Proof.
1.
2.
3.
4. Let us consideris a subgroup?
Prop 3.31:

Definition

Kernel of, Kernel is the preimage of identity:

Lecture 10

Warm-up

=,of G ,is it true that, if




Reformulation:

Coset

Definition

,is the coset of.

Lemma6.3

The following are equivalent(1-3 therioticallt useful, 4 griginal warm-up, 5 How to use this lemma for actual)

Q: Why do we need cosets?
It happens:Example:

Theorem 6.4

H-cosets partition G: we can finda set of elements ofsuch thatthat

Example:
Explain Theorem 6.4 in this case: what are these?
(these are equivalence classes)
Reminder: originally,oriff
The set of equivalence classes:
Set of equivalence classes for the equivalence relationiffis denoted bt(just like)

Theorem 6.10

Lagrange’s Theorem
= finite group,,(Note: all three are natural numbers)

Cor 6.11

,(Remember,= order of=minimals.t.)

Lecture 11

Warm-up

Areandisomorphic?
is a cyclic group andis not, they cannot be isomorphic.The grouphas order 6, butcannot be generated by any single element, and the orders of elements invary.
Also,the number of elements inandare different.
Therefore, as isomorphic groups must have the same structure and element orders,andcannot be isomorphic.
1.is abelian,m butis not.
2.is cyclic, butis not.
3.
, solutions are
, solutions are

Isomorphisms

Definition

Isomorphism is bijective homomorphism.(which is bijective：injective,subjective)

Examples:HW3, Problem 1.7


Q:injective?


eg.

proved
Q:surjective?
is a finite group,of order n:,butfor
, order of

is surjective.

Theorem 9.7+9.8

Ifis a cyclic group, then:
if it is finite order(n), then it is isomorphic to.
if it is of infinite order, then it is isomorphic to.

Thm/Prop

ifare isomorphic, then,then other is.
ifare finite, then,then other is.
ifare cyclic, then,then other is.

(External) Direct Product

Idea: every “object” is easier when it’s decomposed into smaller simple pieces.

Definition

are groups, direct product of&is a setwith the following operation

associativity: check coordinate wise.
identity:
inverses:

Lecture 12

Warm-up

1.What subgroups ofandare normal?
every subgroup ofis normal.()is the generator of


2.Where (0-100) the median( and average) should be for fair grading?
80

Normal Subgroups and Factor/Quotient groups

Definition

,id normal iff
iff

Corollary

ifis abelian, then every subgroup is normal.

Proof:
We have, as
Q: Why do we need the definition of normality
Idea:,, we want group operation on(factor/quotient group of):


such that
Problem: if
How to deal with such sits? Whether

or not.

(Remark:, it is really good!)

First Isomorphism Theorem

Definition

ifis a homomorphism
image of
kernel of

Theorem

ifis a homomorphism, then
(means isomorphic,is bijective)

Sketch of Proof:

1. is normal,
   
   2.To find

Lecture 13

Warm-up

Prove that
Proof.
define a map

is the inertial product of
1.injective
meansor
2.surjective
all of the elements incan be mapped to
3.homomorphism

Correct Proof.

By theorem9.27,

Direct Products

External:



Internal:

Definition

is a group,,is the internal direct product ofandiff
1.(warning:)
2.(i.e. as samll as possible)
3.for any(warning: G is not abelian)

Theorem

ifis internal direct product of, then

(, internal direct product,, external direct product)
Proof.
Let’s consider


Q: is it well-defined?
A:, by 2, we know that

Q:homomorphism?




+surj+inj

Lecture 14

Warm-up

isfinitely generated?
My answer:
No. Prove by contradiction
if it is finitely generated,,, let
Now, consider,it cannot be generated by mutiples ofto, so it cannot be finitely generated
Ans:No
Hint: use induction on m

Abelian World

Fundamental Theorem of Finite Abelian Groups

Every finite abelian groupis isomorphic to, whereare primes andare natural numbers.(is finite rank, the rest are finite piece)

Examples:
, where
, where
, where
, where
Exercise: why?

, where
Proof of the theorem from Milne,Group Theory
“Nonconstructive proofs”: “Assume the opposite” :

$x_1 \in G, Z/p_1^{\alpha_1} =,Z/p_2^{\alpha_2} =,\dots, Z/p_m^{\alpha_m} ={x_1,\ddots, x_m}{y_1,y_2 \ldots, y_m}$

Lecture 15

Warm-up

What is a symmetry of structure? What is structure?
Structure: Structure refers to the set of rules and relationships that govern the elements within a mathematical object. Structure is typically defined by the elements themselves and the operations (such as addition, multiplication) between them, along with the axioms that these operations must satisfy. For example, the structure of a group consists of a set and a binary operation defined on that set, which must satisfy associativity,identity and inverses.

Symmetry of structure: Symmetry refers to transformations that preserve the structure of an object. These transformations are often referred to as “automorphisms,” which are bijective mappings from the object onto itself that preserve its operations. For instance, in geometry, rotating or reflecting a square preserves its shape, and this is an example of geometric symmetry. In algebra, automorphisms of a group are symmetries of the group structure, representing permutations that preserve the group’s operation properties.

Scenario1

n people
everyone votes 0 or 1
How many outcomes?
A:,n+1,2(who wins)
some people know each other


“some situations”=”symmetric situations”

Lecture 16

Review for Midterm I for Group Theory

Groups:abelian, non-abelian
Notation:a finite set with n elements
Sets:
abelian groups:
non-abelian groups:

Lecture 16

Warm-up

what isgeometrically?
Ans:coordinate, usually
?
Then, what about
Abstract Linear Algebra

Permutation Groups

is a set,, is group of all permutations(bijection)

Definition

Permutation group G (on a set) is a subgroup of

Example:

1. for any
2. (last Friday Reading assignment) Cube thing,symmetries of the cube.

Definition

.For each(stabilizer of),

Proposition

Back to Midterm: proper non-abelian subgroup of,

Definition

, Orbit ofunderis the full set

Reminder: “is just a bijective function”

Example2:
Q:What are the-orbits in?
,

Theorem

ifis finite,

Lecture 17

Warm-up

1.
My answer:



2.
My answer:

Group Actions

Definition

“acts on” s the following map:

,s.t.
1.(intuition:“acts” as id)
2.,

Examples:
, like

Proposition

“acts on” by bijections: if you fix anyis a bijection of X

is a function on
Proof.
bijection=injective+surjective
Claim:
(surjective)
assume, if we apply, then bothare in the image.(,)

Proposition

intuition: “act on” is almost the same as, if,s.t., thenis a homomorphism

Lecture 18

Warm-up

acts on (circle with 1 2 3 4 clockwise) by rotations.
1.What is?
2.What isfrom Def2?
3.What isfrom Def1?
Answer:
1.,is “id” rotation,i.e. does nothing.
Choice:“acts by” rotation,.
but also the picture suggests additional structure of “circular order”. i.e. a circle with 1,2,3,4 clockwise.
2., so Def.2:acts on

Group Actions

Proposition

ifwith 1 and 2, then() is homomorphism

By First Isomorphism Theorem for (for):, where hereis the kernel of action
Back to Warm-up:


3.
,

Definition

as a set,.(Left regular action of G on itself)

Theorem9.12

Every group is isomorphic to a group of permutations

Sketch of proof:
(Same as for)

Lecture 19

Warm-up

How many different colorings of a square are there?
My answer:6 or 16

Burnsides’s Lemma

Theorem

is a finite group,is a finite set,acts on(“” is a-set), Then number of-orbits on,where

Remark:all points fixed by whole.
Problem: let’s consider the same square and
a:2013 colors
b:201320132013 colors
How many different coloring do we have?
if two colorings are different by isometry(rigid motions=rotations+reflections) of the square, they’re same.
Idea:Let’s consider situation withcolors,

Header1	Header 2	Header3	Header 4
id	Header 2	H	Header 4
	n	V
	Row 2	Z
	Row 3	Y

X=Set of al possible colorings of the square withcolors
all:
so the-orbits in X is the number of different colorings incolors
all coloring stable under-rotation

Lecture 20

Warm-up

Functions-why?How?


compute:

Motivation for Rings and Fields

Idea: Sometimes we need arithmetic not only with.

Header1
Set
+/-	1+1=2,2-3=-1		1.2+1.2=2.4	usual addition	addition of matrices
Multiplication				you disturbute them	multiplication of matrices
Division	almost never	sometimes	almost always	divisor of polynomials	?not sure
Division Algorithm				division algorithm for polynomials	Do Not commute
Divisors		?	/	divisor algorithm for polynomials
Prime Numbers/gcd		?(ideals)	/	Irreducible polynomials
Euclidean Algorithm	gcd(a,b)=ca+db	?(ideals)	/	Euclidean algo for polynomials

Lecture 21

Last Lecture

Arithmetic,sets+operations
polynomials:division of polynomials.some results fromare generalizable.

HW.Problem1

is generated by transpositions

Rings and Fields

Definition

Ring is a setwith two operations, with 1-6 axioms from the book.
Reformulation:
is an abelian(1) group(2,3,4).
is associative(5).(+ unit for “”)
distributivity:(6)
identity for “+”:0, unit for “”:1.(7)
:is commutative: commutative rings with 1.(8)

Example:

: yes
: yes,
:Yes

: yes
: yes,
:Yes
Q:-inverses?
for, onlyandare invertible.

Answer for the question(-inverses?) for any=greoup of units.(-inversible element of)
for, non-zero numbers are invertible.

Definition

Field is a ringwithand,i.e. ifand, then.

Lecture 22

Warm-up

units ofform a group,find

Definition

A uniti an element s.t.

Definition

Gaussian integers, namely

, because

Definition

A Zero divisor is an element a s.t.

Proposition

For any ring R,

Proof,

on the contrary,

Goal:describe “types” of elements in,Units ofZerodivs ofelse

R	Unit of R	Zerodivs of R	else
			(general phenomenon)

Proposition 16.15

If, then(Cancellation law of non-zerodivisors)

Theorem 16.16

is finite and integral domain, thenis field.

finiteUnits of, nothing else.
integral domain
fieldUnites of=
Exer:is a finite group,, order ofis finite,

Lecture 23

units ofZeroDivisors ofelse
Question: find a ringwith all three nonempty
My answer::

1. det(M)=1invertible
2. 0
3. non-zero but not invertible

Answer:
- non commutative
Direct Product:
, eg., take instead

Division Algorithm for Integral Domains

Theorem 1.1

For any, there exist a pair,, where

eg. 51=6*8+3(a=bq+r)

Theorem 1.2

For anythere exists,where

Example.,
,

Cor(Euclidean Algorithm)

You can compute gcd of 2 polynomials using Thm1.2

Gaussian Integers

Theorem 1.?

for, For any, there exist, where

example:
, find at least 4 pairs of

Lecture 24

Homomorphisms and Ideals

homomorphisms

(means subgroup,means normal subgroup)
First Isomorphism Theorem:







First Isomorphism Theorem:(isomorphism of rings)

Definition

Isomorphismis bijective homomorphism( of rings)

Examples:

Prove thatis homomorphism.
Proof.


is surjective

Definition

(analog of a normal subgroup in Group Theory)
Ideal:inis
a.additive subgroup
b.

Intuition:
is a homomorphism of additive groupsand
Therefore ,is a normal subgroup of

By axioms,is abelian. So any subgroup inis normal

for b:Fact:
. Therefore, if, then
Q for First Isomorphism Theorem for rings: what is? What is?

Definition

A quotient ofbyis a setpf dements

(12)(45)(37)
LCM(2,3)=6,LCM(2,3,4)=12,LCM(2,5,8,10)=40

Lecture 25

Warm-up

prove that


are rings but not fields.
My answer:

1. abelian group
2. associative for
3. distributivity
4. identity for “+” and units for “”

Answer:
1.


but it is not field(is notinvertible)
2.Z[-5]

Z[-5]- integral domain

Lemma

is an integral domain

there no
Proof1.
Assume there exists


Proof2.
, no zero divisors inas no zero divisors in

unitselse

Lemma

is not a unit in

Proof.
Opposite:
Geometric idea:
, not possible

Proposition

Units inare only 1 and -1 becauseif there existss.t., thenis integer
so we have

Definition

(else of) is prime iff ifthenor.

Definition

(else of) is irreducible iff, then eitheroris a unit.

(only divisors ofare units and p itself)

Lemma

3 is not a prime in
3 is irreducible in

Proof.
, but
, if one of them is 1, this is what we claimed.
Then we assumethere is no solution

Lecture 26

Burnside’s Lemma

= finite group,= finite set andacts on, so number of-orbits on=, wherenumber of elements, such thatfixes,.

Problem1

symmetric gtoup on 4 elements(),,
Q:How many orbits? via Burnside’s Lemma.
$\frac{1}{24}(4+62+81)=1$

Problem2

the same group as Problem1,a set of pairswith(is allowed)

Q:How many orbits? via Burnside’s Lemma
$\frac{1}{24}(16+64+81)=2$

Lecture 27

Homomorphisms and Ideals

	Group Theory	Ring Theory
First Homomorphism Theorem
What is this isomorphism
Operation
Why do I talk about equivalent classes	set of equivalent classes foriff	iff
functions	is isomorphism of groups(1.homomorphism of groups, and 2.inj+surj=bij)	with homomorphism of rings plus bijiective= isomorphism of rings
Corollary:Canonical Decomposition of Homomorphisms
	{Kernels of homomorphisms of groups}={normal subgroups}	{Kernels of homomorphisms}={ideals}

Proposition

Proposition

what is happening here?
1.is trivial,
2.is injective

Lecture 28

Warm-up

Isan ideal of(ring of integers) and(polynomials in x with Z coefficient)
is an ideal of, not an ideal of.
Ans:



is not an ideal of, because

Homomorphisms and Ideals III

Reminder:First Isomorphism Theorem for rings:
fix

Question for 11/13:
Whena field?
Question for 11/15:
Whena integral domain?

Proposition

is a field(), then the only ideals inareR$

Proof. Let’s
ifand it’s the only element:
if, then
Reminder: from definition of ideal,, so we have

from Preliminary Problem 1, if()
so we have.
proved

Definition

is a maximal ideal in, there are no

Theorem 16.35

is a commutative ring with,,is a field iffis a maximal ideal in.

Idea: the key tool is Second Isomorphism Theorem.

Second Isomorphism Theorem(16.32)

if, then

So the fieldno proper ideals and proposition above.
Example:

Proposition

is maximal

Proof. opposite, pick, by Euclidean Algorithm,
for

Lecture 29

Warm-up

1.Whyin?
2.What isin?
3.Ifis a ring with only idealsand, thenis a field.
My Answer:
1.
2.inis, or

3.
Step1： Take, considerthen
Step2: Asthen, proved.

Homomorphisms and Ideals IV

Reminder:

Lemma

is an integral domain iffis a prime ideal.

Definition

is prime iffthenor

Proof of the Lemma:
eitheror

Theorem16.38

= commutative ring with, thenis integral domainis prime.

Proof:
$[0]{R/I}=I=0_R+I[a]{R/I} \cdot [b]{R/I}=[0]{R/I} \Rightarrow [a]=[0] or [b]=[0], I \Leftrightarrow a \in Ia \cdot b \in I \Rightarrow a \in Ib \in I$

Corollary

Every maximal ideal is prime. However, in general,

Example:
Last time:is maximal,

Lemma

is prime

ororor, proved

Lecture 30

Warm-up

1.Find all idealss.t.
2.Find all idealss.t.
3.Whyis an ideal?
Ans:

3. additive subgroup and
   , where
   
   ideals in

     graph TD;
    id2["(2)"] --> id6["(6)"];
    id2["(2)"] --> id10["(10)"];
    id3["(3)"] --> id6["(6)"];
    id3["(3)"] --> id15["(15)"];
    id5["(5)"] --> id10["(10)"];
    id5["(5)"] --> id15["(15)"];
    id6["(6)"] --> id30["(30)"];
    id10["(10)"] --> id30["(30)"];
    id15["(15)"] --> id30["(30)"];

Homomorphisms and Ideals V

Definition

commutative ring with, $(x)=={r \cdot x | r \in R}$ is principal ideal generated by x.

Remark: if in, all ideals are principal(andis integral domain), thenis called PID=principal ideal domain.

Definition

commutative ring withideal generated by

Example:

Proposition

a.is an ideal.
b.is a minimal idealsuch that

proof. 2 for a:
1 for a :

Definition

commutative ring withI,J \unlhd R, I \cdot J={i_1 \cdot j_1+\ldots i_m \cdot j_m| i_1 \ldots i_m \in I, j_1,\ldots j_m \in J }$, this is multiplication of ideals.

Notice thatideal generated by, here,is fixed.
However, here the definition of multiplication of ideals,is not fixed.

Proposition

1. $\cdot=$

Lecture 31

Warm-up

why ideals are not scary?
, we knowfor any.
1.Find
2. When $ \subseteq <b,c>?<b,c> \subseteq $
Ans:

1. , the only condition is
   
2. for some
3. for some

Arithm

Lecture 28:toward gnosis
Lecture 29:kairos of arithmetic

• Hw10: Arithmetic Epiphony
  Lecture 30: Arithmetic in Rings V and Arithmetic Metanoia

Lecture 2/09.04
Fundamental Theorem of Arithmetic in Z,, whereare primes
Lecture 20/10.21
Arithmetic in Rings: Division Algorithms and Euclidean Algorithm lead to Fundamental Theorem of Arithmetic
Lecture 22/10.25
Units and Zero-Divisors: 1. Why do arithmetic on “else”.2.Units stand “in front “in Fundamental Theorem or Arithmetic
Lecture 23/10.27
Fundamental Theorem of Arithmetic forare prime
Lecture 25/11.01
1. prime elements and ireeducible elements.2.no FUndamental Theorem of Arithmetic in
Lecture 29/11.18 and Hw10
$a\cdot c=c \leftrightarrow \cdot=\forall \text{ideal} I \unlhd Z[\sqrt{-5}], \exists a_1,a_2 \ldots a_m:I=p_1^{a_1}\ldots p_m^{a_m}p_i\forall (n) \unlhd Z, \exists a, s.t. (n)=(p_1)^{a_1} \ldots (p_m)^{a_m}, (p_i)$ are prime ideals

Lecture 32

Vector Spaces or Linear Algebra in Abstract Algebra

Definition

A vector spaceover F is:

1. an abelian group
2. a multiplication by scalar

here,field =

:

“F”-action
Examples:“algebraically closed”()

Definition

is a linear map,are-vector spaces maps fromto(matrices):

1. homomorphism of abelian groups

Definition

A basis ofofis a set of vectorss.t.

2. are linearly independent.

in basis.

field,

1. is a vector space over.
2. Find basis for

Lecture 34

Warm-up

1.Find multiplicative inverses forin
2.Find multiplicative inverses forin
3.Find multiplicative inverses forinbut as in 2

Fields I

Definition

Field F is 1-8 s.t.andhas multiplicative inverses.

Examples:foris a prime,, like,also

Definition

Extension of fields:is a subfield of K

Example:
subfield=subset+same structures
usually drawn as(from smallest to largest, this arrow contains injective homomorphisms)is the same thing.

Lemma

is a field extension , thenis a vector space over.

1. abelian group
   
2. scalar multiplication
   
   degree of

   Theorem 21.17

   ,

   is a field
   (vector space over Q), butwhere

Lecture 35

Warm-up

Find a minimal polynomial for


Do you remember about minimal/characteristic polynomials in Linear Algebra?
My ans:


is minimal
from preliminary problem 1 from last lecture,butthenas ()
like
However, like, it is wrong since.
if,it is not true.

Field I

| (finite extension)

(this = means asvector space)
let, degree of
So let us choosebasis:

|

(as Q-vector space),
Any

Lemma

is a linear map of E-vector space.

Remark:is not multiplication by scalar. As “Scalar” for E-vector spaces is an element of E, not F.
is “multiplication by a scalar”.
“Proof:”
, distributivity
,commutativity.

Q1: what isin basis(in)?

Lemma

is invertible.(“matrixis invertible”)

Reformulation:

Lecture 36

Field II

, it is the minimal polynomial.
is a field?
, hereis a ring for polynomials(invariable x), withcoefficients.is an ideal ingenerated by a single element,

Proposition

We know thatis a field iffis maximal.
Q:How did we prove maximality of?
79A: Assume, s.t., takebut not in.
asis irreducible in
assume
By Euclidean Algorithm for, where, which caused a contradiction that.
Sois maximal.

Theorem

is a field,is irreducible, thenis a field.

Why would this be useful?
Example0:is a field.
Example:is a field.