Projective Geometry and Transformations of 2D

Planar Geometry

The 2D Projective Plane

Points and Lines

Result 2.1: The pointlies on the lineif and only if.
Result 2.2: The intersection of two lines
Result 2.3: The line determined by two points is
Result 2.6: Duality principle. To any theorem of 2-dimensional projective geometry there corresponds a dual theorem, which may be derived by interchanging the roles of points and lines in the original theorem.

Equation of a conic:

Homogenizing this by replacement,, we have

And its matrix form:

where C is defined as follows,

Five points determines a conic,

And we have,

Result 2.7: The line l is tangent to C at a point x on C is given by l = Cx.

Projective Transformations

transformation of conics

Result 2.13. Under a point transformation, a conictransforms to.
proof:

Dual conic shares the same conclusion.

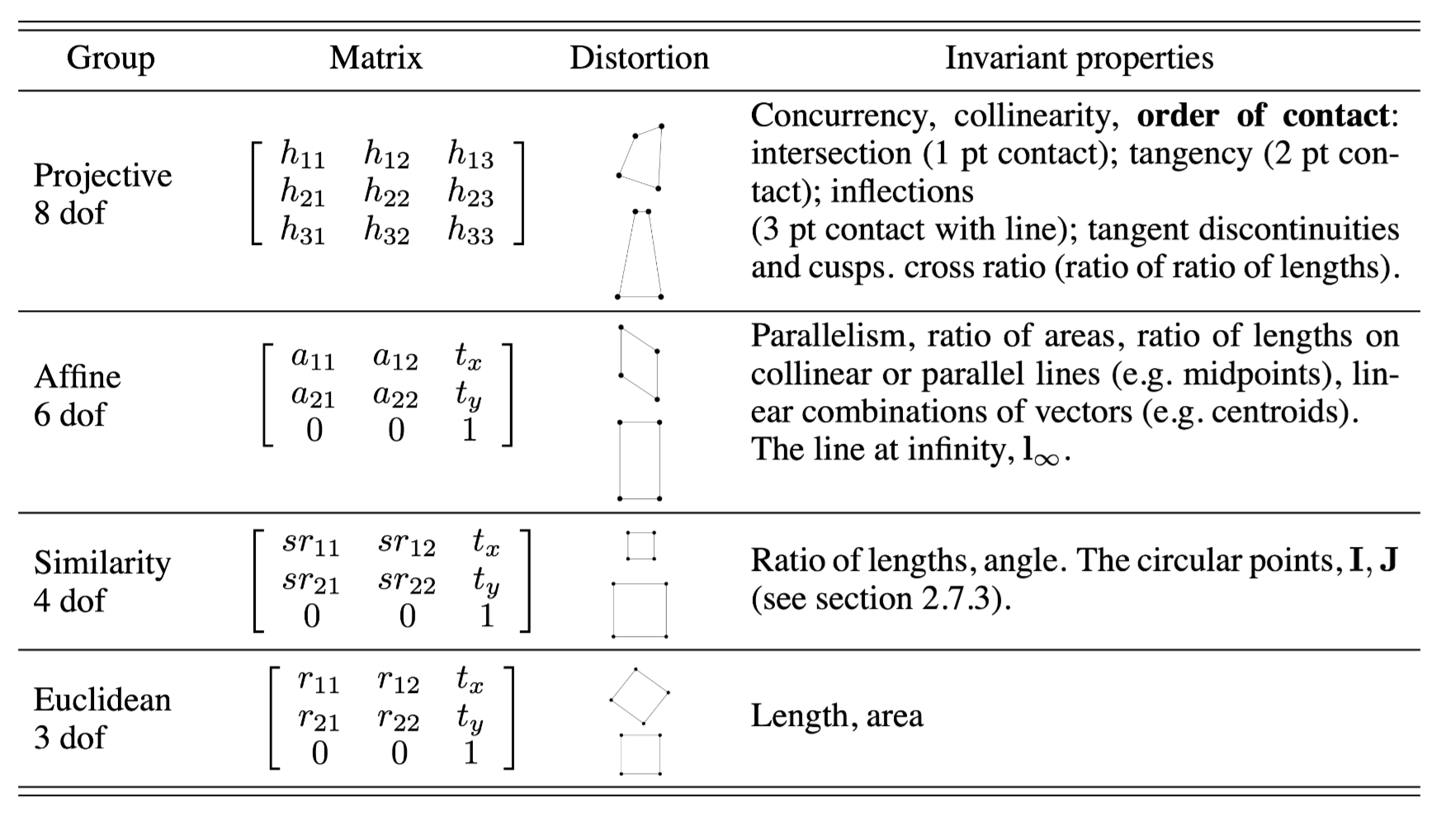
A Hierarchy of Transformation

Decomposition of Projective Transformation

A projective transformation can be decomposed to a series of transformations, where each transformation offers one unique transform different to the former one.

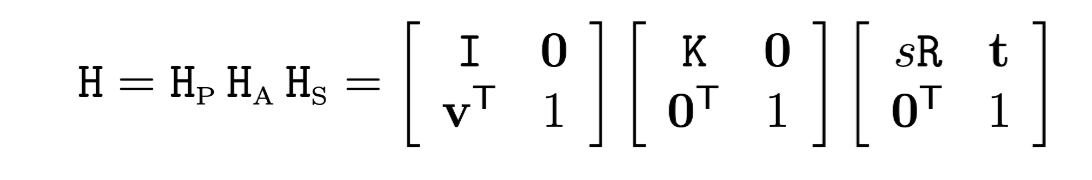
The projective geometry of 1D

Cross Ratio

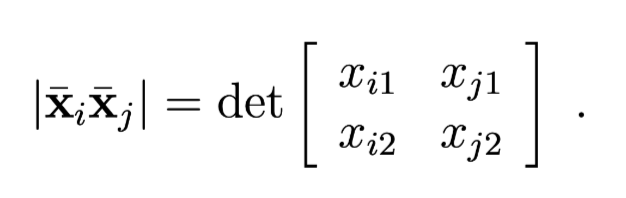
Recovery of affine and metric properties from images

The Line at Infinity

Result 2.17. The line at infinity,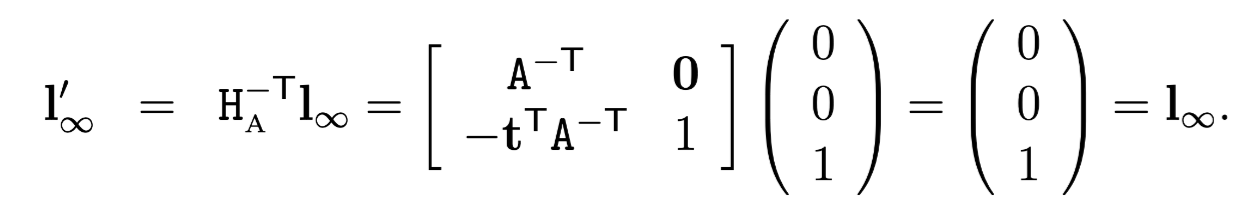, is a fixed line under the projective transformationif and only ifis an affinity.

Recovery of affine properties from images

Once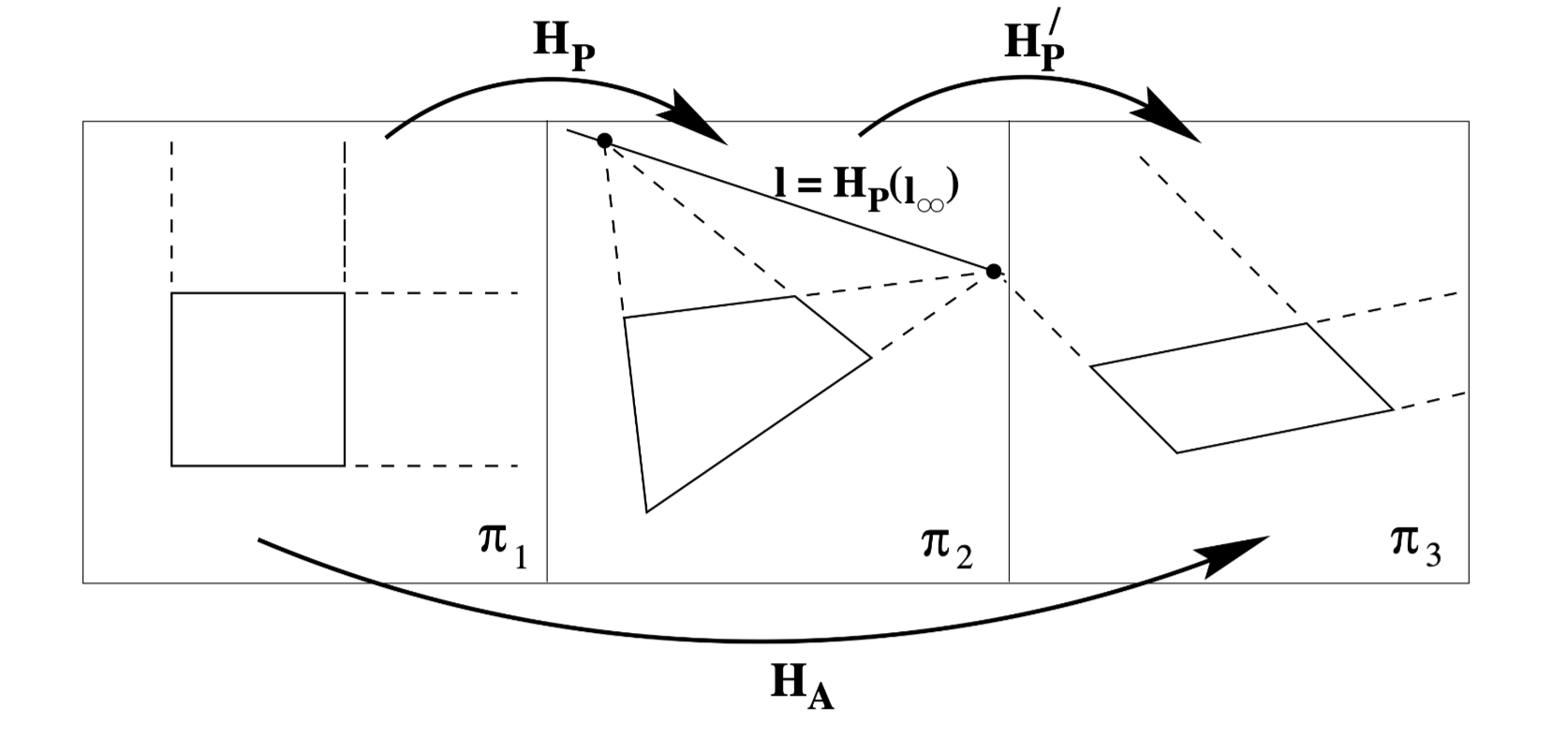is identified a length ratio on a line may be computed from the cross ratio of the three points specifying the lengths together with the intersection of the line with l∞(which provides the fourth point for the cross ratio), and so forth.

Affine properties of the first plane can be measured from the third, i.e. the third plane is within an affinity of the first.

The circular points and their dual

Initially, if the conic is a circle, we have

The conic intersectsat the circular points, where, we have

And we have Algebraically, the circular points are the orthogonal directions of Euclidean geometry,and, packaged into a single complex conjugate entity,

eg.

The conic dual to the circular points is

and we have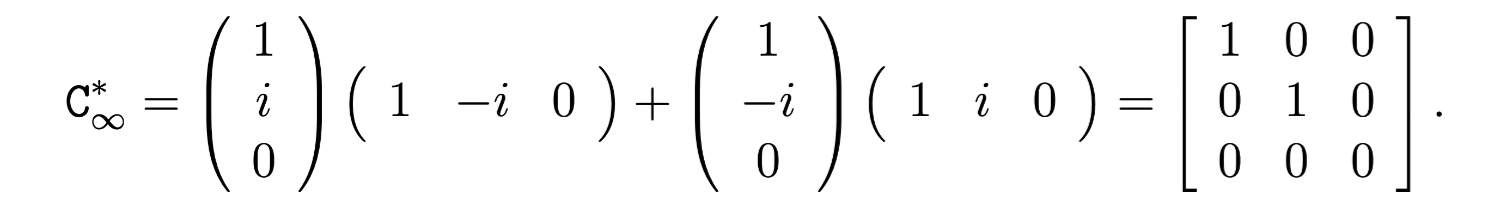

Result 2.22. The dual conicis fixed under the projective transformationif and only ifis a similarity.

Angles on the projective plane

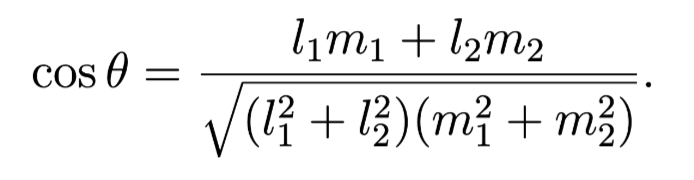
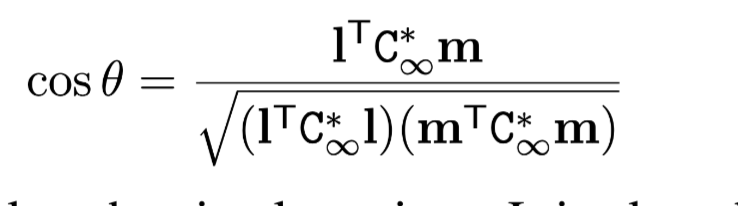
Result 2.23. Once the conicis identified on the projective plane then Euclidean angles may be measured by the formula above.
Proof.

Result 2.24. Linesandare orthogonal if= 0.

Recovery of metric properties from images

According to Result 2.24, we have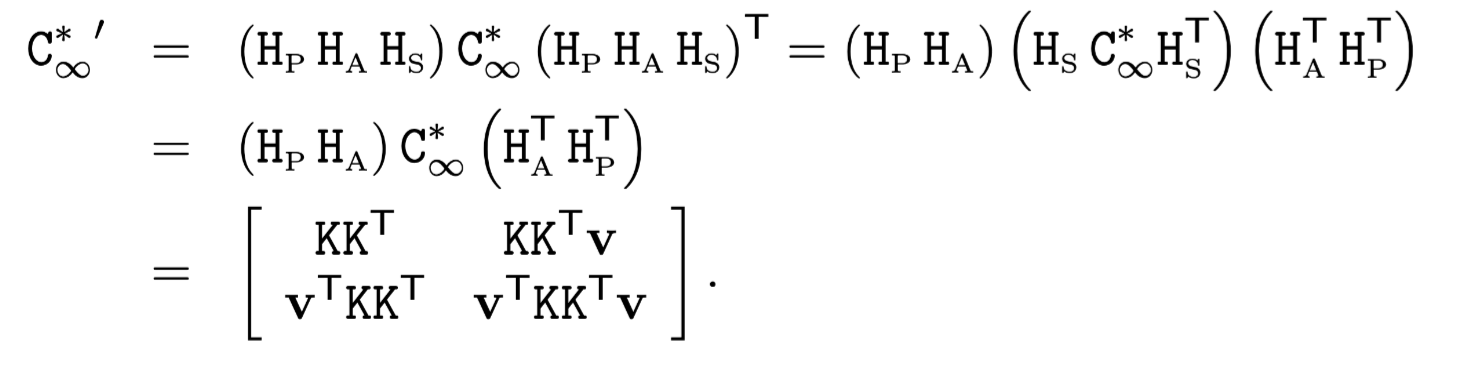

which means that the projective (v) and affine (K) components are determined directly from the image of $C_{\infty}^{}C_{\infty}^{}C_{\infty}^{*} $ is identified on the projective plane then projective distortion may be rectified up to a similarity.
As a matter of fact, by using SVD, we have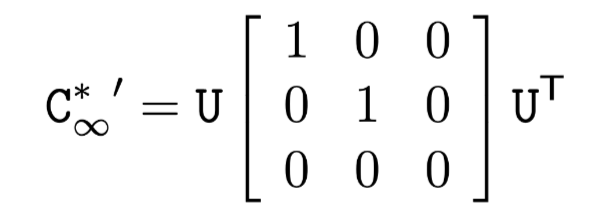

then by inspection from (2.23) the rectifying projectivity is H = U up to a similarity.

Metric rectification I

Suppose the lines,in the affinely rectified image correspond to an orthogonal line pair,on the world plane. From result 2.24= 0, and using (2.23) with v = 0, we have

Here,is a symmetric matrix where. The orthogonality condition reduces the equation which may be written as

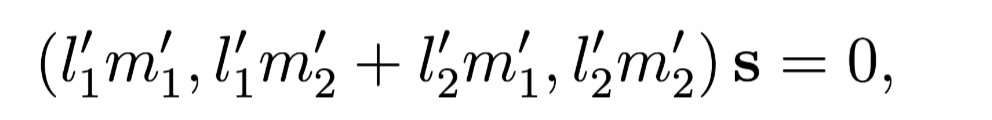
And we can getfrom the equation, futhermoreby using Cholesky Decomposition.

More properties of conics

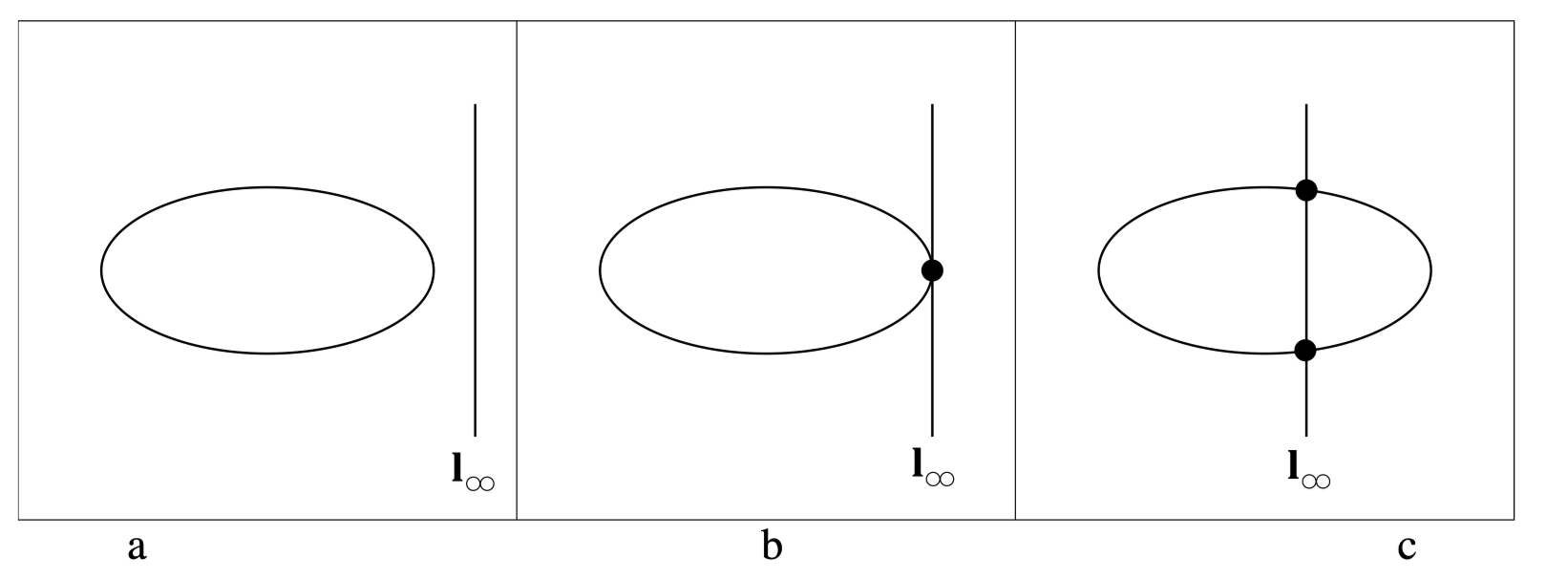
A conic is an (a) ellipse, (b) parabola, or (c) hyperbola; according to whether it (a) has no real intersection, (b) is tangent to (2-point contact), or (c) has 2 real intersections with. Under an affine transformationis a fixed line, and intersections are preserved.
Thus this classification is unaltered by an affinity.

Conclusions

1.use the vanishing line to recover affine properties from images
2.use metric information on the plane, such as right angles, to recover the metric geometry.