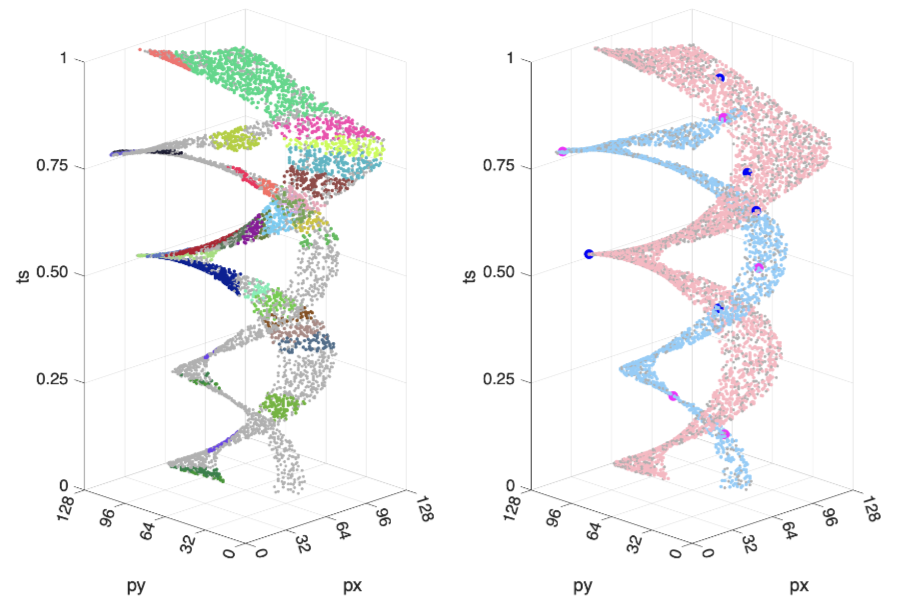
Reading:A 5-Point Minimal Solver for Event Camera Relative Motion Estimation

Original Paper Link:Paper
Paper Auther: Ling Gao* ,Hang Su* ,Daniel Gehrig, Marco Cannici, Davide Scaramuzza, Laurent Kneip

Preliminaries

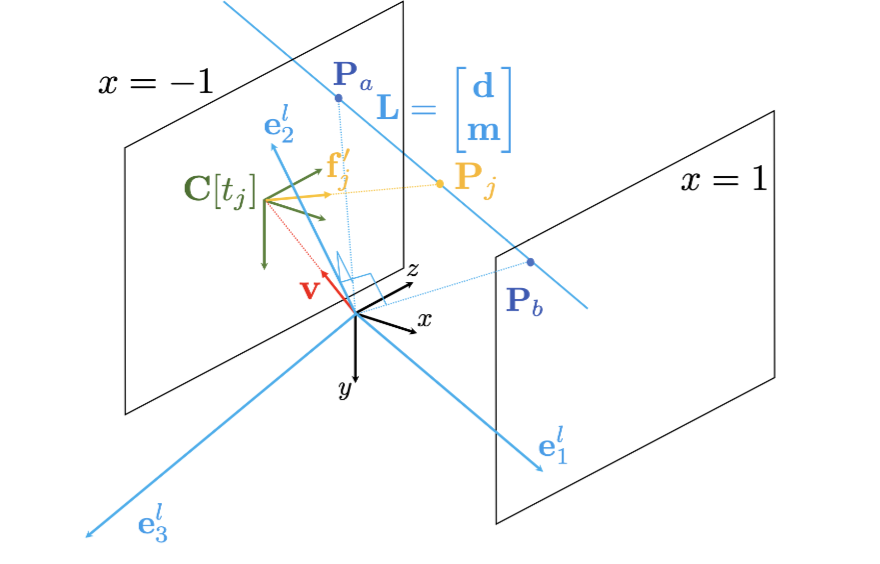
Plucker Coordinates

A Line L can be represented by its direction vector d and a point P

For two nonparallel linesand, we have

Event-based Data Notations

Consider data in, the observed events are given by, where-th event of the-th cluster
Function here projects pointsdefined in the camera frame into the image frame

Converesely have

Andrepresents the translational velocity andrepresents the rotational velocity.

Incidence Relationship

Camera center at time

Rotation from camera frame to reference frame

And we also have

Therefore, the ray can be described in plucker coordinates
$$\left( \left[ \mathbf{R}[t_{ij}] \mathbf{f}{ij} \right]^{\top} \left( \mathbf{C}[t{ij}] \times \left( \mathbf{R}[t_{ij}] \mathbf{f}{ij} \right) \right) \right)^{\top}
\left\langle \mathbf{d}i , \mathbf{C}[t{ij}] \times \left( \mathbf{R}[t{ij}] \mathbf{f}{ij} \right) \right\rangle + \left\langle \mathbf{R}[t{ij}] \mathbf{f}{ij} , \mathbf{m}i \right\rangle = 0
\left\langle \mathbf{d}i , \left( \mathbf{v} \cdot t’{ij} \right) \times \mathbf{f}’{ij} \right\rangle + \left\langle \mathbf{f}’{ij} , \mathbf{m}_i \right\rangle = 0,
$$

Transition to Minimal Form

There are two points in the reference frame

And we define the base of three new directions

Since the velocity in x directions cannot be observed, we have
$$\mathbf{v} = \left[ \mathbf{e}_1^{\ell} \quad \mathbf{e}2^{\ell} \quad \mathbf{e}3^{\ell} \right] \cdot \left[ 0 \quad v_y^{\ell} \quad v_z^{\ell} \right]^{\top} = \mathbf{R}{\ell} \mathbf{v}{\ell}.
t’_j \left( \mathbf{P}b - \mathbf{P}a \right)^{\top} \left( \left( \mathbf{R}{\ell} \mathbf{v}{\ell} \right) \times \mathbf{f}’j \right) - \mathbf{f}’{j} {}^{T}(P_b \times P_a)=0
$$

Five Point Minimal Solver

To remove the scale invariance, an additional constraint on the scale is added. Given that only the structure parameters are affected by the scale invariance, the scale constraint needs to include the related variables. We constrain the scale by adding the equation
$$\left( \mathbf{R}{\ell} \mathbf{v}{\ell} \right)^{\top} \cdot \mathbf{R}{\ell} \mathbf{v}{\ell} - 1 = 0.
\mathbf{v} = \mathbf{e}{1i}^{\ell} \cdot \kappa_i + \mathbf{e}{2i}^{\ell} \cdot v_{yi}^{\ell} + \mathbf{e}{3i}^{\ell} \cdot v{zi}^{\ell}.
\begin{cases}
\mathbf{e}{2i}^{\ell \top} \mathbf{v} = \mathbf{e}{2i}^{\ell \top} \mathbf{e}{1i}^{\ell} \cdot \kappa_i + \mathbf{e}{2i}^{\ell \top} \mathbf{e}{2i}^{\ell} \cdot v{yi}^{\ell} + \mathbf{e}{2i}^{\ell \top} \mathbf{e}{3i}^{\ell} \cdot v_{zi}^{\ell} \
\mathbf{e}{3i}^{\ell \top} \mathbf{v} = \mathbf{e}{3i}^{\ell \top} \mathbf{e}{1i}^{\ell} \cdot \kappa_i + \mathbf{e}{3i}^{\ell \top} \mathbf{e}{2i}^{\ell} \cdot v{yi}^{\ell} + \mathbf{e}{3i}^{\ell \top} \mathbf{e}{3i}^{\ell} \cdot v_{zi}^{\ell}
\end{cases}
\Leftrightarrow
\begin{cases}
\mathbf{e}{2i}^{\ell \top} \mathbf{v} = \left| \mathbf{e}{2i}^{\ell} \right|2^2 \cdot v{yi}^{\ell} \
\mathbf{e}{3i}^{\ell \top} \mathbf{v} = \left| \mathbf{e}{3i}^{\ell} \right|2^2 \cdot v{zi}^{\ell}
\end{cases}
\Leftrightarrow
\begin{cases}
\left| \mathbf{e}{2i}^{\ell} \right|2^{-2} \cdot \mathbf{e}{2i}^{\ell \top} \mathbf{v} = v{yi}^{\ell} \
\left| \mathbf{e}{3i}^{\ell} \right|2^{-2} \cdot \mathbf{e}{3i}^{\ell \top} \mathbf{v} = v{zi}^{\ell}
\end{cases}.
\begin{bmatrix}
\left| \mathbf{e}{21}^{\ell} \right|2^{-2} \cdot \mathbf{e}{21}^{\ell \top} & -v{y1}^{\ell} & \cdots & 0 \
\left| \mathbf{e}{31}^{\ell} \right|2^{-2} \cdot \mathbf{e}{31}^{\ell \top} & -v{z1}^{\ell} & \cdots & 0 \
\vdots & \vdots & \ddots & \vdots & \vdots \
\left| \mathbf{e}{2N}^{\ell} \right|2^{-2} \cdot \mathbf{e}{2N}^{\ell \top} & 0 & \cdots & -v{yN}^{\ell} \
\left| \mathbf{e}{3N}^{\ell} \right|2^{-2} \cdot \mathbf{e}{3N}^{\ell \top} & 0 & \cdots & -v{zN}^{\ell}
\end{bmatrix}
= 0.
[A\quad B][…]=0
= 0, \quad \text{where}
\left[ \mathbf{U} - \mathbf{W} \mathbf{V}^{-1} \mathbf{W}^{\top} \right] \mathbf{v} = 0,
$$